SOAL PERSAMAAN KUADRAT-LINEAR DAN KUADRAT KUADRAT
Nama: SHAQILLA ANDRIANI WIJAYA
Kelas: X IPS 2
Absen: 30
Soal Nomor 1
Penyelesaian dari sistem persamaanadalah
A. dan
B. dan
C. dan
D. dan
E. dan
Pertama, cari titik potong dari grafik keduapersamaan tersebut.
Substitusi nilai ke persamaan , yaitu .
Jadi, penyelesaian sistem persamaan linear-kuadrat tersebut adalah dan .
(Jawaban D)
Soal Nomor 2
Himpunan penyelesaian dari SPLK adalah
A.
B.
C.
D.
E.
Diketahui SPLK
Persamaan dapat ditulis menjadi . Substitusikan pada persamaan .
Jika , maka diperoleh .
Jika , maka diperoleh .
Jadi, HP SPLK tersebut adalah
(Jawaban A)
Soal Nomor 3
Misalkan penyelesaian SPLK adalah dan . Nilai
A. C. E.
B. D.
Diketahui SPLK
Persamaan dapat ditulis menjadi . Substitusikan pada persamaan .
Jika , maka diperoleh .
Jika , maka diperoleh .
Jadi, penyelesaian SPLK tersebut adalah dan , sehingga nilai
Catatan: Karena yang ditanyakan adalah jumlah dari , maka masing-masing nilainya tidak perlu dipermasalahkan bila ditukar-tukar, sebab hasil penjumlahannya pasti sama.
(Jawaban C)
Soal Nomor 4
Titik koordinat yang termasuk penyelesaian dari sistem persamaan adalah
A. D.
B. E.
C.
Pertama, cari titik potong dari grafik keduapersamaan tersebut.
Substitusi masing-masing dua nilai tersebut ke persamaan , sehingga diperoleh
Jadi, titik potongnya adalah dan .
Titik potong adalah titik koordinat yang merupakan penyelesaian dari sistempersamaan tersebut.
(Jawaban B)
Soal Nomor 5
Penyelesaian dari sistem persamaan
adalah
A. dan
B. dan
C. dan
D. dan
E. dan
Ubah persamaan menjadi
Substitusi persamaan pada persamaan . Kita peroleh
Substitusi nilai ke persamaan , yaitu .
Jadi, penyelesaian sistem persamaan linear-kuadrat tersebut adalah dan .
(Jawaban D)
6. Sumbu simetri parabola y = x2 – 5x + 3 diperoleh pada garis …
A. x = 3/2
B. x = 3/2
C. x = 5/2
D. x = 5/2
E. x = 3
Jawaban : D
Pembahasan :
Karena sumbu simetri parabola pasti dilewati oleh titik puncak parabola, maka kita bisa peroleh dengan y’ = 0
Y’ = 2x – 5
0 = 2x – 5
x = 5/2
jadi sumbu simetri parabola y = x2 – 5x + 3 adalah x = 5/2
7. Ordinat titik balik maksimum grafik fungsi y = -x2 – (p – 2)x + (p – 4) adalah 6. Absis titik balik maksimum adalah …
A. –4
B. –2
C. – 1/6
D. 1
E. 5
Jawaban : B
Pembahasan :
NOTE : ordinat = sumbu-y, absis = sumbu-x
Karena berbicara titik balik maksimum, maka kita manfaatkan turunan pertama yaitu y’ = 0
-2x – (p – 2) = 0
-2x = p – 2

8. Nilai minimum fungsi f(x) = x2 – 5x + 4 adalah ….
A. –9/4
B. 9/4
C. 5/2
D. -5/2
E. 4
Jawaban : A
Pembahasan :
Perlu dicatat bahwa nilai maksimum atau minimum suatu fungsi pasti berhubungan dengan turunan pertama yaitu f'(x) = 0
2x – 5 = 0
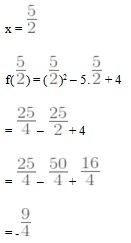
9. Fungsi kuadrat yang grafiknya berpuncak dititik (2, 3) dan melalui titik (-2, 1) adalah …
A. y = -1/8(x – 2)2 + 3
B. y = -1/8(x – 2)2 – 3
C. y = 1/8(x + 2)2 – 3
D. y = 1/8(x + 2)2 + 3
E. y = 1/8(x – 2)2 + 3
Jawaban : A
Pembahasan :
f(x) = ax2 + bx + c
f'(x) = 2ax + b
0 = 2a.2 + b
0 = 4a + b
-b = 4a … (i)
nilai fungsi pada titik puncak
f(2) = a(2)2 + b.2 + c
3 = 4a + 2b + c
3 = -b + 2b + c
3 = b + c … (ii)
f(-2) = a(-2)2 + b(-2) + c
1 = 4a – 2b + c
1 = -b – 2b + c
1 = -3b + c … (iii)
eliminasi persamaan (ii) dan (iii)
b + c = 3
-3b + c = 1 –
4b = 2
b = 1/2
substitusi b = 1/2 ke persamaan (ii)
1/2 + c = 3
c = 5/2
substitusi b = 1/2 ke persamaan (i)
-1/2 = 4a
a = -1/8
f(x) = (-1/8)x2 + 1/2 x + 5/2
= (-1/8)x2 + 4/8 x + 5/2
= -1/8(x2 – 4x) + 5/2
= -1/8(x – 2)2 + 4/8 + 5/2
= -1/8(x – 2)2 + 4/8 + 20/8
= -1/8(x – 2)2 + 3
10. Akar-akar persamaan kuadrat 2x² – 13x + 15 = 0 adalah …
A. 3/2 dan 6
B. 3/2 dan 5
C. 1 dan 6
D. 2 dan 3
E. 2 dan 3/2
Jawaban : B
Pembahasan :
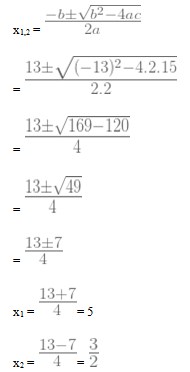
Komentar
Posting Komentar