PERSAMAAN DAN PERTIDAKSAMAAN NILAI MUTLAK
Pengertian
Persamaan nilai mutlak merupakan sebuah persamaan yang selalu bernilai positif. Sedangkan pertidaksamaan nilai mutlak ialah sebuah perbandingan ukuran dua objek atau lebih yang selalu bernilai positif.
1. │f(x)│ = p ↔ f(x) = p atau f(x) = – p,
2. │f(x) │= │g(x) │↔ f(x) = g(x) atau f(x) = – g(x),
│f(x)│ = │g (x) │ ↔ │f(x)│2 = │g(x)│2 ↔ [f(x) +g(x)] [f(x) – g(x)] = 0,
3. a│f(x)│ + b │g(x)│ + c = 0 ,
4. a │f(x)│2 + b │f(x) │ + c = 0 dengan membuat permisalan bahwa │f(x)│ = y
sehingga persamaannya menjadi ay2 + by + c = 0 diperoleh y atau diperoleh │f(x)│
Pertidaksamaan nilai mutlak dalam bentuk:
1. │f(x)│ < p ↔ – p < f(x) < p,
2. │f(x)│ ≤ p ↔ – p ≤ f(x) ≤ p,
3. │f(x)│ > p ↔ f(x) > p atau f(x) < – p,
4. │f(x)│ ≥ p ↔ f(x) ≥ p atau f(x) ≤ – p,
5. │f(x)│< │g (x) │ ↔ │f(x)│2 < │g(x)│2 ↔ [f(x) + g(x)] [f(x) – g(x)] < 0,
6. │f(x)│ ≤ │g (x) │ ↔ │f(x)│2 ≤ │g(x)│2 ↔ [f(x) + g(x)] [f(x) – g(x)] ≤ 0,
7. │f(x)│ > │g (x) │ ↔ │f(x)│2 > │g(x)│2 ↔ [f(x) + g(x)] [f(x) – g(x)] > 0,
8. │f(x)│ ≥ │g (x) │ ↔ │f(x)│2 ≥ │g(x)│2 ↔ [f(x) + g(x)] [f(x) – g(x)] ≥ 0,
9.
10. a │f(x)│2 + b │f(x) │ + c < 0 dengan membuat permisalan bahwa │f(x)│ = y
sehingga persamaannya menjadi ay2 + by + c = 0 diperoleh y atau diperoleh y1 < │f(x)│ < y2 ,
11. a │f(x)│2 + b │f(x) │ + c > 0 dengan membuat permisalan bahwa │f(x)│ = y
sehingga persamaannya menjadi ay2 + by + c = 0 diperoleh y atau diperoleh │f(x)│ < y1 atau │f(x)│ > y2
Contoh soal:
Persamaan
Tentukanlah himpunan penyelesaian |2x – 7| = 3
Jawaban :
|2x – 7| = 3 ( 2x – 7 = 3 ataupun 2x – 7 = -3)
|2x – 7| = 3 ( 2x = 10 ataupun 2x = 4)
|2x – 7| = 3 ( x = 5 ataupun x = 2)
Maka, HP = 2, 5
Pertidaksamaan
Selesaikanlah dari pertidaksamaan | x + 3 | < 2 – x adalah . . .
Jawaban :
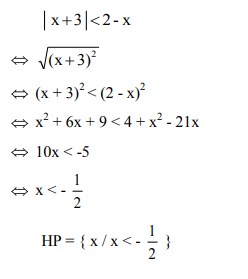
Sekian penjabaran tentang materi persamaan dan pertidaksamaan nilai mutlak dari blog saya. Semoga nilai saya bagus, dan semoga tidak ada kendala saat ibu lizza menilai blog ini aamiin
Nama: shaqilla andriani wijaya
Kelas: X IPS 2
Absen: 30
Komentar
Posting Komentar