SOAL FUNGSI: LINEAR, KUADRAT, RASIONAL, IRASIONAL, DAN GRAFIKNYA SERTA MEMBACA GRAFIKNYA

                      Fungsi linear

1. Umur pak Andi 28 tahun lebih tua dari umur Amira. Umur bu Andi 6 tahun lebih muda dari umur pak Andi. Jika jumlah umur pak Andi, bu Andi, dan Amira 119 tahun, maka jumlah umur Amira dan bu Andi adalah …. tahun

A. 86 

B. 74 

C. 68 

D. 64

E. 58

Jawaban : C

Pembahasan : 

Misalkan Umur Pak Andi=x, umur Amira=y dan umur Ibu Andi=z

x = 28 + y …(1)

z = x – 6; atau x=z+6 …(2)

x + y + z = 119 …(3)

dengan melakukan operasi penjumlahan (1) pada (2) didapatkan

2x = y + z + 34 atau 2x – y – z = 34 …(4)

Lakukan operasi penambahan (3) pada (4) atau

x + y + z = 119

2x – y – z = 34

3x =153

Atau

x = 51

Dengan melakukan substitusi x pada (1) dan (2) didapatkan

Y = 23; z = 45

Sehingga

jumlah umur Amira (y) dan bu Andi (z) adalah y + z = 23 + 45 = 68

2. Himpunan penyelesaian sistem pertidaksamaan

5x + y ≥ 10

2x + y ≤ 8

        y ≥ 2

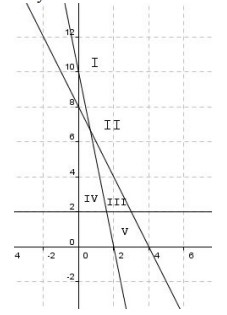
ditunjukkan oleh daerah . . .

A. I

B. II

C. III

D. IV

E. V

Jawaban : C

Pembahasan : 

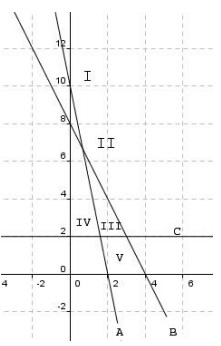
• Terlihat pada gambar bahwa A adalah persamaan garis 5x + y = 10 titik potong dengan sumbu x jika y = 0

x = 2 → titik (2,0)

titk potong dengan sumbu y jika x = 0

y = 10 → titik (0,10)

daerah 5x + y ≥ 10 berada pada garis persamaan tersebut dan di atas garis (I, II,III, V) —(a)

• B adalah persamaan garis 2x + y = 8 titik potong dengan sumbu x jika y=0 x = 4 → (4,0)

titik potong dengan sumbu y jika x = 0 y = 8 → (0,8)

daerah 2x + y ≤ 8 berada pada garis persamaan tersebut dan di bawah garis (III, V) ….(b)

•  C adalah garis y = 2

daerah di atas garis y = 2 adalah I, II, III, IV …(b)

dari (a) , (b) dan (c) :

• 1) I II III V
• 2) III V
• 3) I II III IV

Yang memenuhi ketiga-tiganya adalah daerah III

Jawaban : C

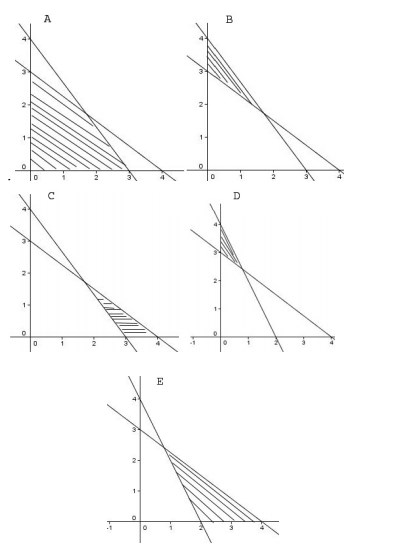
3. Himpunan penyelesaian pertidaksamaan- pertidaksamaan 2x+y≥ 4 ; 3x + 4y ≤ 12, x ≥ 0, y ≥ 0 dapat digambarkan dengan bagian bidang yang diarsir sebagai berikut : 

Jawaban : E

Pembahasan : 

2x + y ≥ 4 ;

2x + y = 4

titik potong dengan sumbu x , y = 0

x = 2 → (2,0)

titik potong dengan sumbu y, x = 0

y = 4 → (0,4)

3x + 4y ≤ 12

3x + 4y = 12

titik potong dengan sumbu x, y = 0

x = 4 → (4,0)

titik potong dengan sumbu y, x = 0

y=3 → (0,3)

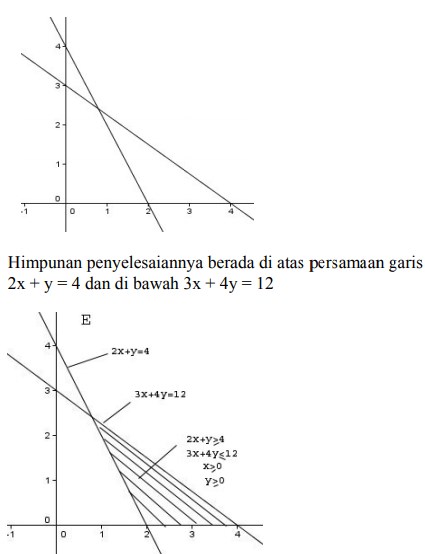
Jawaban : E

4. Daerah yang diarsir merupakan himpunan penyelesaian dari sistem pertidaksamaan linear… 

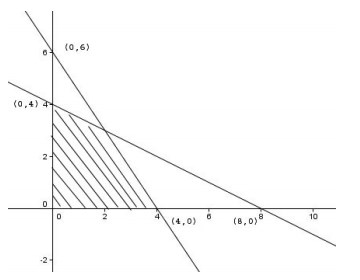
A. x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0

B. x + 2y ≥ 8, 3x + 2y ≥ 12, x ≥ 0, y ≥ 0

C. x – 2y ≥ 8, 3x – 2y ≤ 12, x ≥ 0, y ≥ 0

D. x + 2y ≤ 8, 3x – 2y ≥ 12, x ≥ 0, y ≥ 0

E. x + 2y ≤ 8, 3x + 2y ≥ 12, x ≥ 0, y ≥ 0

Jawaban : A

Pembahasan : 

karena daerah arsiran dibawah persamaan garis maka

x + 2y ≤ 8 ….(2)

Arsiran di atas sumbu x dan di kanan sumbu y maka x ≥ 0 dan y≥ 0 ….(3) dan (4)

sehingga daerah penyelesaiannya adalah:

(1), (2), (3) dan (4)

3x + 2y ≤ 12, x + 2y ≤ 8 dan x≥ 0, y≥ 0

Jawaban : A

5. Daerah yang diarsir pada gambar di bawah adalah himpunan penyelesaian dari sistem pertidaksamaan… 

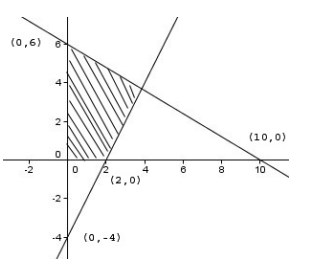
A. 5x + 3y ≤ 30, x – 2y ≥ 4, x ≥ 0, y ≥ 0

B. 5x + 3y ≤ 30, x – 2y ≤ 4, x ≥ 0, y ≥ 0

C. 3x + 5y ≤ 30, 2x – y ≥ 4, x ≥ 0, y ≥ 0

D. 3x + 5y ≤ 30, 2x – y ≤ 4, x ≥ 0, y ≥ 0

E. 3x + 5y ≥ 30, 2x – y ≤ 4, x ≥ 0, y ≥ 0

Jawaban : D

Pembahasan : 



                       Fungsi kuadrat

Soal Nomor 1
Koordinat titik balik grafik fungsi kuadrat $f\left(x\right)=2x^2-4x+5$ adalah $\cdots \cdot$
A. $(1,3)$                       D. $(2,5)$
B. $(1,5)$                       E. $(2,7)$
C. $(1,7)$

Pembahasan

Karena $f\left(x\right)=2x^2-4x+5$, berarti $a=2,b=-4,c=5$.
Absis titik balik dinyatakan oleh
$x_p=-\frac{b}{2a}=-\frac{-4}{2\left(2\right)}=1$
Substitusikan $x=1$ pada $f\left(x\right)=2x^2-4x+5$, sehingga diperoleh
$y_p=f\left(1\right)=2(1{)}^2-4(1)+5=3$
Jadi, koordinat titik balik grafik fungsi kuadratnya adalah 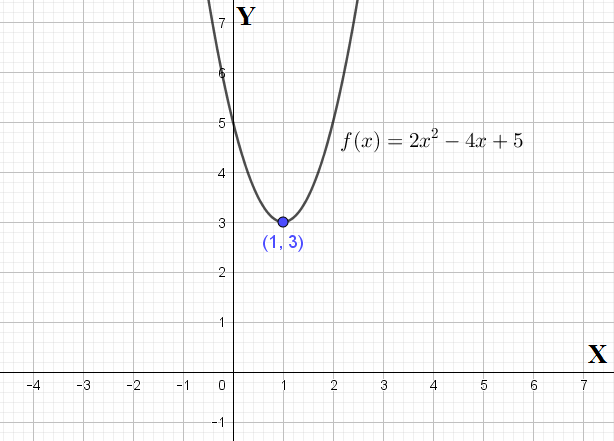$(x_p,y_p)=(1,3)$

(Jawaban A)

Soal Nomor 2
Diketahui fungsi kuadrat $f\left(x\right)=2x^2-7x-5$serta titik $A(2,-11)$, $B(-1,0)$, dan $C(-4,55)$. Titik yang dilalui grafik fungsi $f\left(x\right)$ adalah $\cdots \cdot$
A. titik $A,B$, dan $C$
B. titik $A$ dan $B$
C. titik $A$ dan $C$
D. titik $A$ saja
E. titik $C$ saja

Pembahasan

Titik $P(x,y)$ dilalui oleh grafik fungsi $f\left(x\right)$apabila substitusi nilai $x$ pada rumus fungsi menghasilkan nilai $y$.
Diketahui $f\left(x\right)=2x^2-7x-5$.
Periksa titik $A(2,-11)$:
Substitusi $x=2$ pada $f\left(x\right)$, diperoleh
$\begin{array}{cc}f\left(2\right)& =2(2{)}^2-7(2)-5\\ & =8-14-5=-11\end{array}$
Diperoleh $y=-11$ sehingga titik $A$ dilalui oleh grafik fungsi $f\left(x\right)$.
Periksa titik $B(-1,0)$:
Substitusi $x=-1$ pada $f\left(x\right)$, diperoleh
$\begin{array}{cc}f(-1)& =2(-1{)}^2-7(-1)-5\\ & =2+7-5=4\end{array}$
Diperoleh $y=4$ sehingga titik $B$ tidak dilalui oleh grafik fungsi $f\left(x\right)$.
Periksa titik $C(-4,55)$:
Substitusi $x=-4$ pada $f\left(x\right)$, diperoleh
$\begin{array}{cc}f(-4)& =2(-4{)}^2-7(-4)-5\\ & =32+28-5=55\end{array}$
Diperoleh $y=55$ sehingga titik $C$ dilalui oleh grafik fungsi $f\left(x\right)$.
Jadi, titik yang dilalui adalah titik $A$ dan $C$.
(Jawaban C)

Soal Nomor 3
Jika gambar di bawah merupakan grafik fungsi kuadrat $f$ dengan titik puncak $(-2,-1)$ dan melalui titik $(0,-5)$, maka nilai $f\left(2\right)$ adalah $\cdots \cdot$

A. $-17$                      D. $-20$
B. $-18$                      E. $-21$
C. $-19$

Pembahasan

Rumus fungsi kuadrat bila berpuncak di $(x_p,y_p)$ dan melalui titik $(x,y)$ diberikan oleh
$y-y_p=a(x-x_p{)}^2$
Diketahui $x_p=-2,y_p=-1,x=0$, dan $y=-5$, sehingga didapat
$\begin{array}{cc}-5-(-1)& =a(0-(-2){)}^2\\ -4& =a(2{)}^2\\ a& =-1\end{array}$
Untuk itu, rumus fungsi kuadratnya menjadi
$y=a(x-x_p{)}^2+y_p\Rightarrow y=-(x+2{)}^2+1$
Untuk $x=2$, diperoleh
$\begin{array}{cc}f\left(2\right)=y& =-(2+2{)}^2-5\\ & =-4^2+1=-17\end{array}$
(Jawaban A)

Soal Nomor 4
Diketahui fungsi kuadrat $f\left(x\right)=-2x^2+4x+3$dengan daerah asal $\{x|2\le x<3,x\in R\}$. Daerah hasil fungsi $f$ adalah $\cdots \cdot$
A. $\{y|-3\le y\le 5,y\in R\}$
B. $\{y|-3\le y\le 3,y\in R\}$
C. $\{y|-13\le y\le -3,y\in R\}$
D. $\{y|-13\le y\le 3,y\in R\}$
E. $\{y|-13\le y\le 5,y\in R\}$

Pembahasan

Diketahui $f\left(x\right)=-2x^2+4x+3$.
Absis grafik dari fungsi kuadrat itu adalah
$x_p=-\frac{b}{2a}=-\frac{4}{2(-2)}=1$
Karena koefisien $x^2$ bernilai negatif, maka parabola akan terbuka ke bawah. Di titik $x=1$, nilai maksimum fungsi akan tercapai, yaitu
$\begin{array}{cc}f\left(1\right)& =-2(1{)}^2+4(1)+3\\ & =-2+4+3=5\end{array}$
Nilai minimum fungsi pada interval $-2\le x\le 3$ tercapai pada nilai $x$ yang paling jauh jaraknya dari $x=1$, yaitu $x=-2$, sehingga
$\begin{array}{cc}f(-2)& =-2(-2{)}^2+4(-2)+3\\ & =-8-8+3=-13\end{array}$
Dengan demikian, daerah hasil fungsi $f$ adalah $\{y|-13\le y\le 5,y\in R\}$
(Jawaban E)

Soal Nomor 5
Fungsi kuadrat yang grafiknya melalui titik $(-1,3)$dan titik baliknya sama dengan titik balik dari grafik $f\left(x\right)=x^2+4x+3$ adalah $\cdots \cdot$
A. $y=4x^2+x+3$
B. $y=x^2-3x+1$
C. $y=4x^2+16x+15$
D. $y=4x^2+15x+16$
E. $y=x^2-3x-1$

Pembahasan

Koordinat titik balik dari grafik $f\left(x\right)=x^2+4x+3$ adalah
$\begin{array}{cc}{x}_p& =-\frac{b}{2a}=-\frac{4}{2\left(1\right)}=-2\\ y_p& =(-2{)}^2+4(-2)+3=-1\end{array}$
Jadi, koordinat titik baliknya adalah $(-2,-1)$.
Rumus fungsi kuadrat bila berpuncak di $(x_p,y_p)$ dan melalui titik $(x,y)$ diberikan oleh
$y-y_p=a(x-x_p{)}^2$
Diketahui $x_p=-2,y_p=-1,x=-1$, dan $y=3$, sehingga didapat
$\begin{array}{cc}3-(-1)& =a(-1-(-2){)}^2\\ 4& =a(1{)}^2\\ a& =4\end{array}$
Substitusi balik $x_p=-2,y_p=-1,a=4$sehingga didapat
$\begin{array}{cc}y-(-1)& =4(x-(-2){)}^2\\ y+1& =4(x^2+4x+4)\\ y& =4x^2+16x+15\end{array}$
Jadi, rumus fungsi kuadratnya adalah $f\left(x\right)=y=4x^2+16x+15$
(Jawaban C)

                      Fungsi rasional

Soal nomor 1

Tentukan dy/dx dari fungsi implisit y berikut.

x3−xy+y3=1

Pembahasan

Diferensialkan setiap suku terhadap x.
d/dx(x3)−d/dx(xy)+d/dx(y3)=d/dx(1)

3x2−(x dy/dx+y)+3y2 dy/dx=0

(−x+3y2) dy/dx+3x2−y=0

dy/dx=y−3x2/3y2−x

Jadi, diperoleh dy/dx = 3x²/ 3y²-x